Algorithmic Complexity

Logistics

Please make sure you have emailed your github account to Josh.

Pseudocode

It is often useful to use pseudocode when we discuss algorithms. This helps us gloss over syntax details and get to the heart of a problem. It is often helpful to plan in pseudocode before writing. There is no strict syntax for pseudocode, but here are some suggstions:

no need to declare variables or worry about type
no punctuation necessary
be complete–don’t skip steps
use indentation and ALLCAPS for organization.

Here’s an example:

FOR X = 1 to 10 
    FOR Y = 1 to 10 
        IF gameBoard[X][Y] = 0 
            Do nothing 
        ELSE 
            CALL theCall(X, Y) (recursive method) 
            increment counter

Complexity

There are many features that make a good algorithm * Speed * Space used * Lines of Code * Clarity

Let’s focus on speed.

Computers are very fast, so speed is not a problem for small datasets. For larger data sets, however, a slow algorithm will make a difference. We could look at the difference by writing two algorithms and testing. Or we can analyze them independent of implementation. Consider the following problem:

arrayMax(A,n):
  input: An array A storing n>=1 integers
  output: The maximum element in A

We can define an solution as follows:

arrayMax(A,n):
  currentMax = A[0]
  FOR i : 1 --> n-1
    IF currentMax < A[i]
      currentMax=A[i]
  RETURN currentMax

What is the best case? What is the worst case? For this algorithm there are 1 + 2*(n-1) + 1 primitive operations in the worst case.

Big O notation describes the limiting behavior of a function, usually in terms of simpler functions. We say that arrayMax is O(n).

Big O

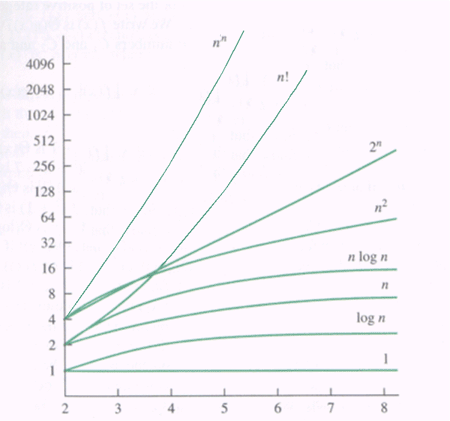
graph

notation	Name	examples
O(c)	constant	determining if a number is even or odd
O(log n)	logarithmic	finding an item in a sorted array
O(n)	linear	finding an item in an unsorted array
O(n log n)	loglinear	sorting
O(n^2)	quadratic	all pairs of of elements
O(n^c)	polynomial	all subsets of N elements
O(c^n)	exponential	traveling salesman problem
O(n!)	factorial	all permutations of N elements

Sorting

The visuals here are wikimedia commons

bubble sort

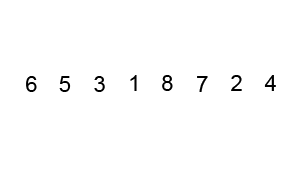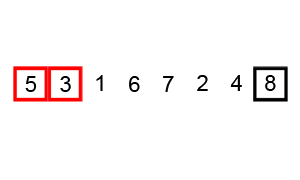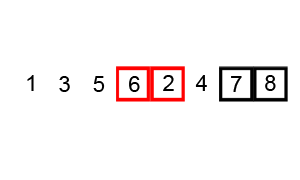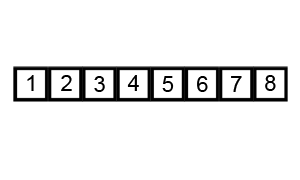
First Pass:
( 5 1 4 2 8 ) \to ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps since 5 > 1.
( 1 5 4 2 8 ) \to ( 1 4 5 2 8 ), Swap since 5 > 4
( 1 4 5 2 8 ) \to ( 1 4 2 5 8 ), Swap since 5 > 2
( 1 4 2 5 8 ) \to ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.
Second Pass:
( 1 4 2 5 8 ) \to ( 1 4 2 5 8 )
( 1 4 2 5 8 ) \to ( 1 2 4 5 8 ), Swap since 4 > 2
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )
Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.
Third Pass:
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )

video

selection sort

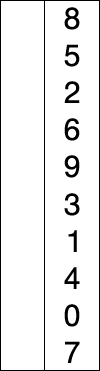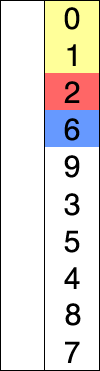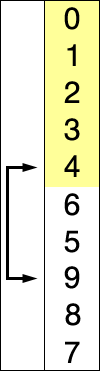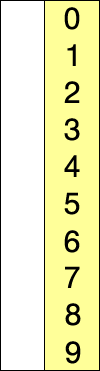
64 25 12 22 11 // this is the initial, starting state of the array
11 25 12 22 64 // sorted sublist = {11}
11 12 25 22 64 // sorted sublist = {11, 12}
11 12 22 25 64 // sorted sublist = {11, 12, 22}
11 12 22 25 64 // sorted sublist = {11, 12, 22, 25}
11 12 22 25 64 // sorted sublist = {11, 12, 22, 25, 64}

video

insertion sort

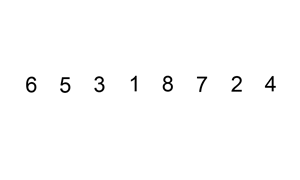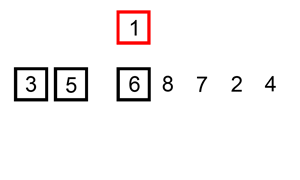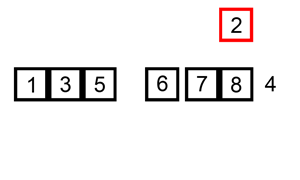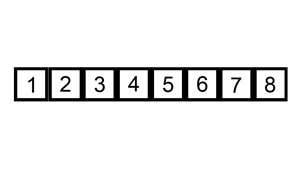
becomes

video

3 7 4 9 5 2 6 1
3 7 4 9 5 2 6 1
3 7 4 9 5 2 6 1
3 4 7 9 5 2 6 1
3 4 7 9 5 2 6 1
3 4 5 7 9 2 6 1
2 3 4 5 7 9 6 1
2 3 4 5 6 7 9 1
1 2 3 4 5 6 7 9

merge sort

video

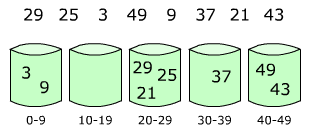
bucket sort

assorted videos

listening to sort

bubblesort Csángó

Sort Demos

demos

assignment

The content for this assignment is distributed individually

I recommend you do the problems in this order:

Name in Readme
formatting error
div by 2
big O
sorting
whatsort
fix mergesort

also in the issues, there is some filename confusion:

divby2.txt is problem1.txt
bigo.md is problem2.md
sorting.md is problem3.md
whatsort.txt is problem4.txt